Bagsmrita Bhagawati (1)
Labananda Choudhury (2)

(1) Assistant Professor in Statistics B. H. College, Howly, Assam, India.
(2) Professor, Department of Statistics, Gauhati University, Assam, India

Correspondence:
Dr. Bagsmrita Bhagawati Assistant Professor in Statistics B. H. College,
Howly, Assam,
India.
Phone: 9435736550.
Email: bagsmritasarma28@gmail.com

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Introduction
The study of mortality in India during the first part of the twentieth century forms a very important and interesting study. It is very significant to note that India's population growth in those years i. e. from 1901 to 1951 was governed not by the fluctuations in the birth rate but by the wide variations in the death rate. Thus death rate, not birth rate determines the population trend in India. In those earliest years of the twentieth century, the population was constant or declined as a result of great catastrophe like famine, epidemic, war or at times, a combination of all these. Even though at some point of time the Indian populace was exempted from the aforementioned calamities, it was however constantly being the prey of poor diet which very significantly determined the mortality patterns of the country. The change in population is also negligibly influenced by impact of emigration. The study of mortality is increasingly being necessary to examine the past and future population trends of India. (Davis, K., 1961). This kind of work requires a long time series of data which subsequently enables one to trace the demographic history of a birth cohort, that is, the group of persons born in a given year. ( Bourbeau, et.al. ,2004). Here comes the importance of construction of generation life tables.

Life tables are one of such vital statistical models through which transition pattern of mortality can be explained. A life table has been universally regarded as a concise way of showing the ability of a member of a particular populace existing or disappearing at a particular age. Life tables do not require standard population for comparing mortality like other measures of mortality. The levels and trends in mortality depict the change in the quality of life of a population. The community health employees, researchers, planners and many more from other allied disciplines utilize life table notion and method in their study. (Kintner, 2004). Stating the importance of life tables Coale and Demeny (1966) opine "Life tables provide a succinct description of what is the most prominent aspect of the state of human mortality; they show the varying chances of dying as a function of age."

Life table can be categorized into two types according to the reference year - period or current life table and generation or cohort life table. The period life table demonstrates the collective mortality experience by age of the people living in an area. It describes the mortality pattern prevailing in a particular short period such as one or three years. The second type of life table i.e. the generation life table consists of mortality rates experienced by a particular birth cohort, in which the age specific death rates of that cohort from their birth through each consecutive age in successive calendar years are used. This kind of life table requires data for a long period, at least for 100 years. This requirement of data for a longer period put hurdles in constructing generation life tables. Hence one generally prefers construction of period life table instead of generation life tables. However, generation life tables have their own share of significance in projecting actual mortality transition. Generation life table is useful for projections of mortality, for study of mortality trends, and for the measurement of fertility and re-productivity (Kintner, 2004). Hence, more precisely, the generation life tables can be used to compute generation reproduction rates, to study life expectancy historically, to project mortality, and to make estimates of orphanhood (Gregory, 1965). In this way, generation life tables help to study the mortality trends in a population more specifically since they are based on the different combinations of age specific death rates.

Dublin and Spiegelman (1941), Dublin, Lotka and Spiegelman (1949), Spiegelman (1957) and others study generation life tables with great results. A number of countries viz. Germany (Bomsdorf, 1993), England and Wales (Case, 1962), Australia (Lancaster,1959; Young,1969), Belgium (Veys,1981), France (Delaporte, 1941; Vallin, 1973), the Netherlands (Tas, 1991; Van Poppel, 1996), Sweden (Schoen and Urton 1979; Bolander,1970), the United States (Jacobson, 1964), Thailand (Prasartkul and Rakchanyaban, 2002), Canada and Quebec (Bourbeau.et.al, 2004) construct generation life tables. However in India due to a dearth of reliable data on mortality, period life tables are usually preferred instead of generation life tables. However, the period life table has certain problems in reflecting proper mortality pattern. This method understates the mortality status as it believes in a unitary set of health conditions. The generation life table, on the other hand, could represent the development of life expectancy of real cohorts since it believes in changing mortality status over the years. Willets (1999), (2004), Richards and Jones (2004), Richards et al. (2006) and many others also discuss the importance of birth cohorts for studying the pace of mortality.

The aforesaid discussion prompts one to construct sex-wise generation life table for India. This will further help one to examine the influence of different birth cohorts on distribution of age at death.

Objectives
The objectives of this paper are:
1. to construct sex wise generation life table of India for 1901 to 1951, for birth cohorts 10 years apart.
2. to assert the advantage of generation life expectancy over period life expectancy by computing the magnitude of the gap between the two life expectancies.
3. to examine the effects of different birth cohorts on distribution of age at death for male and female population of India.

Data and Methodology
It has already been mentioned that the key focus of this work is to trace the mortality trend of India for the period 1901 to 1951 by constructing a generation life table. Justifications for use of generation life table has partly been offered in the introduction and widely been discussed throughout this paper. Though it is possible to construct generation life table for any birth cohort, this study earmarked the period from 1901 to 1951 with specific reasons. It is considered that the pre twentieth century data for India are seemingly hazy and unreliable and beyond 1951, data become too dependent on projections.

The data used in this study are secondary and the unavailability of reliable data for such a long period of time justifies the use of different sources of secondary data for constructing the generation life tables. Murray et.al (2003) has supported the use of different sources of data to estimate mortality in countries like India, China and Brazil where different sources including surveillance systems, vital registration and surveys are used. Here we do not go for smoothing of the data since in this study of generation life table; the emphasis is to establish its closeness to the actual data than to remove the fluctuations if any. (Kintner, 2004). The different steps required for constructing generation life tables are discussed in the following:

Computing and estimating life expectancies at birth:
The first step in constructing generation life table is to obtain and estimate the trends of sex wise period life expectancies at birth eo. In this work eo are obtained for population of India during the 20th and first half of the 21st century (1901 to 2051) from the available data. For instance, the construction of a generation life table of 1901 requires life expectancy at birth for 100 years i.e. for 1901,1902, 1906 and then for every 5 year intervals, 1911,1916 so on up to 2001. This will provide information for ages 0, 1, 5, 10 ,.... and so on as in the case of abridged life table. The generation life tables of 1911, 1921, 1931, 1941 and 1951 will follow the similar pattern.
In this work the data on life expectancy at birth for the male and female population of India is taken from life tables constructed by Malaker and Roy (1990), reports published by the office of the Registrar General of India (Sample Registration System reports: 1989-93, 1994-98 and 1999-2003), CBHI (Central Bureau of Health Intelligence, 2005) and life expectancy at birth projections made by Mahmood and Kundu (2006). The generation life tables of this study are based on a set of life expectancy at birth available for the periods covered as shown below:

Period 1901-1971:
The life expectancy at birth from 1901, 1911 to 1971, i.e. for every 10 year intervals were obtained from CBHI (Central Bureau of Health Intelligence, 2005).

Period 1902-1952 and for the year 1980:
The life expectancy at birth for the years 1902, 1912, 1922, 1932, 1942, 1952 and 1980 were estimated from the available period life tables by assuming a uniform annual increment or decrement of expectation of life at birth. The Registrar General of India used to estimate life expectancy at birth using Sample Registration System (SRS) data for some states of India. These estimates are derived from the clubbed data for a period of five years of Age Specific Mortality Rate and published in SRS abridged life tables. The estimates for the period 1998-02 may be referred to the mid period 2000. This is illustrated as follows: If life expectancy at birth increases by 3.8 years during 1991-2000, then it gains at about 0.38 years annually. (SRS based on abridged life table 2002-06). This incites us to assume that life expectancy at birth increases/decreases uniformly annually.

Period 1906-1986:
The mid period life expectancy i.e. for 1906, 1916 to 1986, i.e. for every 10 year interval, was not available in CBHI and hence taken from life tables constructed by Malaker and Roy (1990). Malaker and Roy reconstructed life tables for India from 1901-11 to 1971-81 and projected for 1981-91 and 1991-2001. Further the mortality pattern observed in the life tables of Malaker and Roy (1990) is similar to the sample registration system and thereby validates the use of the life tables of Malaker and Roy in this study.

Period 1991-2001:
The life expectancy at birth for the years 1991, 1996 and 2001 were obtained directly from period life tables of 1989-93, 1994-98 and 1999-2003 constructed by Register General of India, using Sample Registration System. (SRS Analytical Studies, Report No. 1 of 1996, report No.3 of 2003 and report No.1 of 2006).

Period 2006-2051:
The life expectancy at birth from 2006 to 2051 was taken from the projections made by Mahmood and Kundu (2006). The rationale behind the use of this projection is that it projects population of India by using component method of projection, similar to Mari Bhat (2001) who projects population of India around the year 2025 by using the same method. The base year in the former case is provided by the census of India 2001 whereas Mari Bhat considers it to be 2000, on the basis of the provisional results of the 2001 census. The life expectancy at birth of the male and female population of India for the year 2011 is 65.77 and 67.95 years respectively according to the 2011 census. (Office of the Registrar General and Census Commissioner, 2011), and the corresponding eo in 2011 estimated by Mahmood and Kundu (2006) are 65.48 and 68.95 respectively. This may provide necessary justification in support of using this projection for constructing generation life table. With the help of the aforementioned sources we have obtained and estimated the different life expectancies at birth for the male and female population of India.

The life expectancies as shown in figure 1 represent the pattern of mortality evolution of population of India during the 20th and the first half of the 21st century.

Figure 1: Trend of eo from 1901-2051, India, males and females


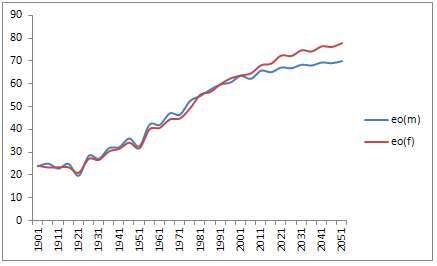
Table 1: Estimated Sex wise Life expectancies at birth, India, 1901-2051


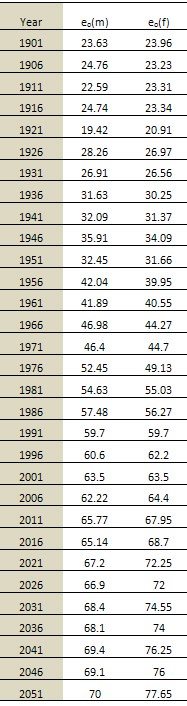
The above table and figures track the general trend of mortality by computing expectation of life at birth for the males and females of India from 1901 to 2051. It is observed that eo ranges between 19 and 78 years during the 20th and first half of the 21st century. In the beginning of the twentieth century males and females of India were subjected to excess mortality due to prevalence of epidemics, floods, famines and war or a blending of all these. The first half of the twentieth century witnessed the influenza endemic of 1918 which increased the annual death rate to 63 per thousand. But after this calamity, death rate was never too high and it started declining gradually. The infant mortality rate was also high in 1918. It was 267 per thousand life births and a gradual decline thereafter. Though such decline in infant mortality rate is not parallel to the general mortality rate; the fall in the infant mortality contributed a major share to the reduction in general mortality. (Davis,K. 1951). Further, data from Sample Registration System indicates that Crude Death Rate of India declined from 14.9 in 1971 to 7.6 in 2005. The infant mortality rate of India also declined from 115 per thousand live births in 1961 to 53 in 2008. (Sample Registration System, 2001). This transformation of mortality over the years influenced the expectation of life at birth. The present study also observes that between 1901 and 2051, female birth cohorts' life expectancy at birth is more than three times in India rising from 24 years to 78 years. However the gains for males were smaller than the females, with life expectancy at birth of males rising only from 24 years to 70 years between the same cohorts. The present and future females of India thus would have higher life expectancy at birth than the males. Bourbeau et al (2004) too observe higher life expectancies at birth among females of Canada and Quebec than the males. From figure 1 it is seen that the gap between life expectancy at birth for the two sexes remained almost negligible in the twentieth century. However the 21st century female cohorts have considerably improved their probability of survival compared to those of the male cohorts. The gap between life expectancy at birth for the two sexes of India rose to 1 year for the 1911 cohort to 8 years for the 2051 cohort. An Indian female in the 2051 cohort would, therefore, expect to live 8 years longer than her male counterpart. Bourbeau et al (2004) also find that the gap between life expectancy at birth for the two sexes rose from 5 years for the 1901 cohort to 8 years for the 1941 cohort for Canada.

Derivation of nqx from the above estimated eo:
These computed eo are now used to obtain the probability of death by age (nqx). In India period life tables are not available for every year of this study. Hence model life tables are used. The model life tables are also used by the United Nations population Division and the World Bank from their estimated and extrapolated life expectancies. Out of the four Coale and Demeny regional model life able, we use here West model life table. The table covers countries of Western Europe and the non-European population. This model is the representative of the general mortality pattern since it is derived from the largest and broadest variety of cases. In general, the West families of the Coale- Demeny model produce better overall fit to the data especially at the younger ages, 0-15 years. (Coale and Demeny,1966). And in our country, the age group is most unpredictable. In 1982 the United Nations published a set of model life tables for developing countries. But in this study the life expectancy at birth does not match with any of the five regions prepared by the United Nations. Hence it catalyses this work to use West model life table in studying mortality trends. The following formula as suggested by Keyfitz for which period life table is unavailable is used for obtaining a comparable set of model life tables for each sex with the same level of life expectancy at birth as that of the individual states. This formula is also discussed by Kohli (1977). Also this notion is partially used by Andreev, E et al (1985) in obtaining distribution of mean life expectancy of 100,000 randomly chosen pairs on the 81 points with a maximum difference in eo of 3 years. Mahmood and Kundu (2006) also observed that the figure of eo is very helpful for selecting suitable model life table for a country for which a reliable life table is not available.

The formula to obtain the probability of death is discussed as follows:

The weight W is obtained as


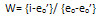
Where i stands for expectation of life at birth of an individual state and eo and eo' are the upper and lower limits of the expectation of life at birth of the West model life table.

The new set of qx'' values is obtained by


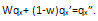
qx and qx' are the observed values for the above expectation of life at birth of the model life table.

The last age used in these mortality data is 100. Hence we apply mortality law l(x) = C* ab to extrapolate survivors in a life table beyond the last age as discussed by Preston et al (2001). Parameters C, a and b can be estimated from the last three values of the life table survival function, l(y), l(y+n) and l(y+2n).(Horiuchi and Coale,1982). We have

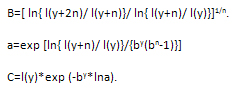
Now nqx is obtained from the above extrapolated lx values by using nqx = ndx/lx

The nqx for the years 1921 and 1941 are obtained directly from the life tables constructed by Davis (1951). In his study life tables are constructed for males and females of India for 1911-21 and 1931-41. The nqx for the years 1991, 1996 and 2001 were obtained directly from the period life tables of 1989-93, 1994-98 and 1999-2003 as published by the office of the Registrar General of India. (SRS Analytical Studies, Report No. 1 of 1996, report No.3 of 2003 and report No.1 of 2006).

Arrangement of nqx by age and calendar years:
These nqx are to be arranged by age and calendar years to represent the mortality schedule at corresponding ages of each birth cohort. Figure 2 explains the procedure of transformation of nqx presenting the nqx of 1901 generation life table. The examples are as follows:

1q0 of the cohort born in 1901 is the 1q0 in the 1901 period life table,
4q1 of the cohort born in 1901 is the 4q1 in the 1902 period life table,
5q5 of the cohort born in 1901 is the 5q5 in the 1906 period life table,
5q90 of the cohort born in 1901 is the 5q90 in the 1991 period life table,
and 5q100 of the cohort born in1901 is equal 1.

Figure 2: Transformation of nqx from period to cohort life tables


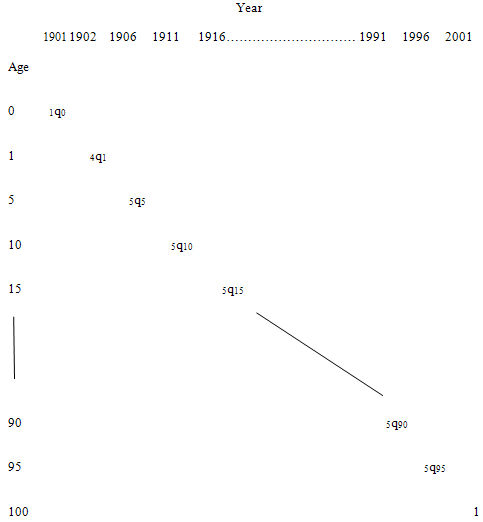
Figure 3: Generation probabilities of death (nqx) across different birth cohorts of males of India


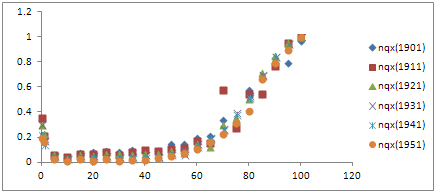
Figure 4: Generation probabilities of death (nqx) across different birth cohorts of females of India


Figures 3 and 4 (as shown above) represent the generation probabilities of death by age, sex and birth cohort. In general, the probability of dying for all ages has fallen for both males and females since the 1901 cohort. However, a generalized excess mortality among males and females are observed for the 1911 cohort. This decade 1911-21 recorded the highest decade mortality rate due to the ravages of the 1918-19 influenza epidemic (Davis, K. ,1951). In 1918 influenza alone claimed 12 million lives in India. Further plague, smallpox, cholera, etc. also catalyzed the high mortality during this period. The severe droughts in 1911, 1913, 1915, 1918 and 1920 also increased the death toll. The First World War (1914-18) also claimed the lives of thousands of Indian soldiers. However after 1921, improvement in health and sanitation conditions controlled occurrences of epidemics to some extent. These resulted in declining death rate. The diminishing trends of death rate were also achieved as a result of improvement in transportation which subsequently facilitates distribution of food during drought and flood across the country (Census of India 1911 and 1921). The shape of the curve (in figures 3 and 4) representing the probability of dying at different ages has changed little over the generations for both males and females. The probability curve for the 1911 male cohort shows up a bump at age 70 whereas there was no such bump for female cohort, probably death was not sufficiently significant among female cohorts to change the shape of the curve.

Calculation of other columns of the life table:
Other columns of the life table can be described as follows:
Year: 1901-2001.
Age: 0-100.
ndx : Number of deaths in the cohort between ages x and x+n.
ndx = nqx * lx
lx : Number of survivors to age x in the cohort.
l0=100000.
nLx : is the number of person years lived in the cohort between ages x and x+n.

According to Reed and Merrell Lx may be obtained from the following equations for ages under 10.

L0=0.276lo+0.724l1
4L1=0.034l0+1.184l1+2.782l5
5L5=-0.003l0+2.242l5+2.761l10
Greville (1943) observed that method given by Reed and Merrell is a particular case and suggested the following formula when n is equal
nLx =n/2(lx+lx+n)+n/24(ndx+n-ndx-n)
For last age 100, L100=l100 (log10l100).
Tx : Person years lived above age x.

Tx= nLx
ex : Expectation of life at age x.
ex = Tx/ lx.
This lead to construction of sex wise generation life tables of India for the years 1901, 1911 to 1951, every 10 years apart as depicted in tables 2 to 4.

Calculation of gap:
Gap is computed by
Gap=Cohort life expectancy at birth - period life expectancy at birth (Goldstein and Wachter, 2006). This gap will reflect the change in mortality pattern over time by studying the differences between period and cohort life expectancy at birth across cohorts as shown in Table 5.

Distribution of age at death for 60+ or aged to study the effects of different cohorts:
Distribution of age at death=db,x/db,mode (Richards, 2008)
db,x and db,mode are the number of deaths at age x and number of deaths at the modal age at death for birth cohort b respectively. This ratio will take the peak value one at the modal age at death i.e. at age having maximum number of deaths as portrayed in Tables 6 and 7.

Results and Conclusions
The construction of generation life table informs about the general mortality trends prevailing among male and female populations of India. Tables 2 to 4 represent the generation life table for birth cohort 1901 to 1951 i. e. cohorts born every 10 years of intervals for male and female population of India. These tables help in studying the mortality transition of people residing in this part of the world.

The generation life expectancies are calculated by allowing changes in mortality rates in coming years and are hence considered as the more appropriate measure to know about a person's expectation of life. (Kintner, 2004). Table 5 depicts the variation between period and cohort life expectancy at birth by computing gaps. In India gaps rise from about 1 year in 1901 to 12 years in 1951 among its male members. Its female counterpart's gap is slightly less than one year in 1901 to about 14 years in 1951. Thus we may observe that the variation between period and cohort life expectancies has lengthened over time and it may increase further for both of its male and female populations of India. Prasartkul and Rakchanyaban (2002) also observed such a kind of gap among the male and female population of Thailand. The generation life table for the cohort of U.S females born in 1900 also added nearly 10 years to its life expectation at birth of 58.3 years in contrast to the expectation of life at birth of period life table of 49 years (Bell et al., 1992). The cohort life expectancy at birth is greater than its corresponding period life table since mortality decreases across the years. The gaps as computed in columns 4 and 7 of table 5 are the bonus years received by the cohort from taking advantage of future mortality improvement. From the same table we may observe that the period life expectancy at birth in 1941 and 1951 is 32 and 31 years for males and females respectively. This is the same as generation life expectancy at birth in 1931. Hence there is a past cohort with the same summary measure of mortality as given by the period life table. The plausible reason of this variation may be that the generation life tables are used to study the development of mortality and life expectancy of real cohorts over time. This type of table studies the mortality improvement for the actual cohort for a long period of time whereas period life table understate this improvement. The generation life table considers the changing intra cohort influence on health whereas period table considers only the single mortality improvement pattern and unitary set of health condition (Kintner, 2004). The amount of gap portrays the pace of mortality improvement across time. In other words the pace of decline in mortality plays an important role in determining the magnitude of gap (Goldstein and Wachter 2006). Thus the generation life table paves new avenues to study the mortality status of people residing in India.

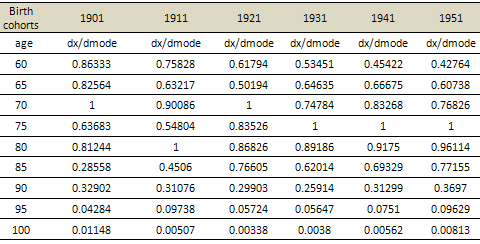
Tables 6 and 7 show that the birth cohorts of 1901 to 1921 have the modal age at death at age 70 and for birth cohorts of 1931 onwards the modal age is at age 75 both for male and female populations of India. Here we observed a contrast peak value of 1 at age 80 for female birth cohort of 1911. The peak value 1 at higher ages depicts that most deaths fall at older ages. This ratio of db,x/db,mode also indicates the tendency of increasing longevity by year of birth i.e. fewer premature deaths among the elderly population of India, with rising birth cohorts. Richards (2008) also observed that for modern populations of England and Wales, most deaths fall at older ages, the peak value will be after age 70 years.

Tables
Different tables have been provided in this section.

Table 2: Sex Wise Generation Life table of India for 1901 and 1911

Table 3: Sex Wise Generation Life table of India for 1921 and 1931


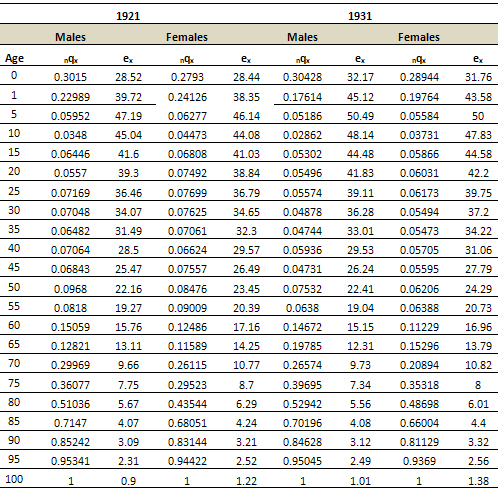
Table 4: Sex Wise Generation Life table of India for 1941 and 1951


Table 5: Gap between generation and period life expectancy at birth


Table 6: Distribution of deaths by age at different birth cohorts for male population of India


Table 7: Distribution of deaths by age at different birth cohorts for female population of India


References
Andreev, E. Lutz, W. Scherbov, S. (1989) Averaging Life Expectancy International Institute for Applied Systems Analysis, W P-89-35.
Bell, F., A. Wade, and Goss, S.(1992) Life tables for the United States social Security Area 1900-2080. Actuarial Study, No.107. Office of the Actuary, U.S. Social Security Administration. SSA Pub. No. 11-11536.
Bhat, M. Indian Demographic Scenario, 2025· (2001) Population Research Centre, Institute of Economic Growth, Delhi.
Bolander, A.M. (1970). A study of cohort mortality in the past hundred years in cohort mortality of Sweden, three studies describing past, present, and future trends in mortality, National Central Bureau of Statistics, Statistical Report, pp. 5-51.
Bomsdorf, E., (1993). Future Developments in Mortality and Life Expectancy among Birth Cohorts of 1903-1993, Germany, in Zeitschrift fur Bevolkerungswissenschaft, Vol.19, No. 1, pp. 93-103.
Case, R.A.M. and al. (1962). Chester Beatty Research Institute Serial Abridged Life Tables: England and Wales, 1841-1960, The Chester Beatty Research Insitute, London.
Census of India 1911, 1921 2001, 2011, RGI, GOI, http://www.censusindia.gov.in/2011- prov-results-paper1-india.html.
Central Bureau of Health Intelligence, (CBHI), (2005) National Health Profile, Govt. of India.
Coale, A. J. and Demeny, P. (1966), Regional Model Life Tables and Stable Populations, Princeton: Princeton University Press.
Davis, Kingsley: (1951).The Population of India and Pakistan, Princeton : Princeton University Press.
Delaporte, P. (1941). "Évolution de la mortalité en Europe depuis les origines des statistiques de l'état civil", Étude démographique No. 2, Paris, Imprimerie nationale, 156 pages.
Dublin L.I., and Spiegelman, M (1941). "Current Versus Generation Life Tables", Human Biology,13:439-458.
Dublin L.I., Lotka, A.J. and Spiegelman, M (1949). Length of Life. Rev. ed. New York: Ronald Press.
Goldstein, J.R. and Wachter, K.W. (2006), Gaps and Lags: Relationships between Period and Cohort Life Expectancy, Population Studies, March 2006.
Gregory, I. (1965)." Retrospective Estimates of Orphanhood from Generation Life Tables." Milbank Memorial Fund Quarterly 43(3):323-348.
Greville, T.N.E. (1943). "Short Methods of Constructing Abridged Life Tables", The Record of the American Institute of Actuaries. Col. XXXII, Part 1, No. 65 (June).
Horiuchi, S and Coale, A.J. (1982)." A Simple Equation for Estimating the Expectation of Life at Old Ages," Population Studies,36(2):317-26.
Jacobson, P.H.(1964). "Cohort Survival for Generations Since 1840." Milbank Memorial Fund Quarterly 42(3):36-51.
Keyfitz, N, A Note on Model Life Tables,(Mimeographed), as cited by Kohli, K.L. (1977) Mortality in India, a Statewise Study, Sterling Publishers (Pvt.) Ltd. Page, 98.
Kintner, H.J. (2004). The Life Table. In: Siegel, J.S. and Swanson, D.A. (eds.). The methods and materials of demography, 2nd edition. San Diego: Elsevier, Academic Press: 301-340.
Kohli, K.L. (1977) Mortality in India, a Statewise Study, Sterling Publishers (Pvt.) Ltd.
Lancaster, H.O. (1959). "Generation Life Tables for Australia", Australian Journal of Statistics, No. 1.
Mahmood, A and Kundu, A (2006): "Demographic Projections for India 2006-2051: Regional variations". Draft prepared for the IWMI-CPWF project on Strategic Analysis of National River Linking Project of India.
Malaker, C.R. and Roy, S. Guha. (1990), Reconstruction of Indian Life Tables for 1901-1981 and Projections for 1981-2001, Sankhya: the Indian Journal of Statistics volume 52, series b, pt. 3, pp. 271-286.
Murray CJL, Ferguson BD, Lopez, A. D. Guillot M, Salomon JA, Ahmad OB,(2003) Modified logit life table system: principles, empirical validation, and application, Population Studies, Vol. 57, No. 2, pp. 165-182.
Pearl, R. and Reed. L.J. (1920), On the rate of growth of the population of the United States since 1790 and its mathematical representation, Proceedings of the National Academy of Sciences 6, 275-288
Prasartkul ,P and Rakchanyaban, U; (2002) Estimated Generation Life Tables for Thailand of Five-Year Birth Cohorts:1900-2000. IPSR Publication No.261.
Preston, S.H., Heuveline, P., and Guillot, M. (2001) Demography, Measuring and Modeling population Processes. Blackwell publishers Ltd,Oxford,UK.
Richards, S. J. and Jones, G. L. (2004) Financial Aspects of Longevity Risk. London: Staple Inn Actuarial Society.
Richards, S. J., (2008): Detecting year-of-birth mortality patterns with limited data, J. R. Statist. Soc. A, 171, Part 1, pp. 279-298.
Richards, S. J., Kirkby, J.G. and Currie, I.D. (2006) The importance of year of birth in two-dimensional mortality data. Br. Act. J., 12, 5-61.
Schoen, R. and Urton, W. L. (1979). Marital Status Life Tables for Sweden, Years1911-1973 and Cohorts Born 1885/89-1940/44, Urval, Published by the National Central Bureau of Statistics, Stockholm, No. 10, 272 pages.
SRS based Abridged Life Tables 1989-93, 1994-98 and 1999-2003 SRS Analytical Studies, Report No. 1 of 1996, SRS Analytical Studies, Report No. 3 of 2003 and SRS Analytical Studies, Report No. 1 of 2006; Registrar General, India New Delhi.
SRS based Abridged Life Tables 2002-06 Office of the Registrar General, India New Delhi.
Sample Registration System (2001): Office of the Registrar General, India New Delhi.
Tas, R.F.J. (1991). "Cohort Life Tables for the Netherlands by Age and Sex Derived from Observations during the Period 1860-1989", Maandstatistiek Van de Bevolking, Netherlands, Vol. 39, No. 6, pp. 15-26.
United Nations (1982)). Model Life Tables for Developing Countries. United Nations Publication, Sales No. E.81.X111.7.
Vallin, J. (1973). La mortalité par génération en France depuis (1899), Paris, PressesUniversitaires de France, INED, Cahier No. 63, 483 pages.
Van P., Frans, Tabeau, E. and Willekens, F. (1996). "Trends and Sex Differentials in Dutch Mortality Since 1850: Insights from a Cohort- and Period-Perspective", Genus, Vol. LII, No. 3-4, Luglio-December, pp. 107-134.
Veys, D. (1981). "De sterftetafels, transversaal en longitudinaal, in België", Bevolking en Gezin, No. 2, pp. 205-227.
Willets, R. C. (1999) Mortality in the Next Millennium, Staple Inn Actuarial Society, London.
Willets, R. C. (2004) The cohort effect: insights and explanations. Br. Act. J., 10, 833-877.
Young, C.M. (1969). An Analysis of the Population Growth and Mortality of Selected Birth Cohorts in Australia, Ph.D Thesis, Department of Demography, Australian National University, Canberra.